پاییز ۱۹۷۲، ونس فابر بهعنوان استاد جدید در دانشگاه کلرادو مشغول به کار شد. فابر با پاول اردوش و لازلو لواز، دو ریاضیدان با نفوذ دیگر، ملاقات کرد. اردوش و فابر و لواز دربارهی ابرگرافها بحث کردند. در آن زمان، ابرگراف ایدهی جدیدی در نظریهی گراف بود. پس از کمی بحث، آنان به پرسشی واحد دست یافتند که بعدها با عنوان احتمال اردوش و فابر ولواز شناخته شد. این احتمال دربارهی حداقل تعداد رنگهای موردنیاز برای رنگآمیزی یالهای ابرگرافهای موجود در محدودههای مشخص بود. فابر گفت:
این مسئله سادهترین احتمالی بود که میتوانستیم به آن برسیم. کمی روی آن کار کردیم و به این نتیجه رسیدیم که تا فردا آن را حل خواهیم کرد؛ اما این اتفاق هرگز رخ نداد.
احتمال بهدستآمده دشوارتر از حد انتظار بود. اردوش این احتمال را یکی از سه احتمال دلخواهش عنوان کرد و پاداشی برای حلش در نظر گرفت که با افزایش دشواری مسئله به پانصد دلار رسید. مسئله در نظریهی گراف شناخته و برای حلش تلاشهای زیادی شد؛ ولی هیچکدام موفق نبودند.
حالا پس از پنجاه سال، گروهی شامل پنج ریاضیدان درنهایت احتمال اردوش و لواز و فابر را اثبات کردند. آنان در مقالهی پیشانتشارشان که ژانویه منتشر شد، محدودیتی برای تعداد رنگهای موردنیاز بهمنظور سایهزنی یالهای ابرگرافهای معین قرار دادند؛ بهطوریکه هیچ یال همپوشانی رنگ یکسان نداشته باشد. آنان ثابت کردند تعداد رنگها هرگز بیشتر از تعداد رأسهای موجود در ابرگراف نخواهد شد.
روش مدنظر کنارگذاشتن برخی یالهای گراف و رنگآمیزی تصادفی دیگر یالها را شامل میشود؛ ترکیبی از ایدههایی که پژوهشگران در سالهای اخیر برای حل تعدادی از مسائل دشوار در نظر گرفته بودند. در آن زمان، این روش دردسترس اردوش و فابر و لواز نبود؛ اما حالا دو ریاضیدان بازمانده از آن زمان میتوانند از نوآوریهای ریاضی کنونی لذت ببرند.
رنگهای کافی
اردوش و فابر و لواز درحالیکه چای میخوردند و دربارهی ریاضیات بحث میکردند، به ساختار جدید گرافمانندی در ذهنشان رسیدند. گرافهای ساده از نقاطی به نام رأس ساخته شدند که با خطوطی به نام یال به یکدیگر وصل میشوند. هر یال دقیقا دو رأس را به یکدیگر وصل میکند؛ اما ابرگرافهای اردوش و فابر و لواز محدودیت کمتری دارند؛ یعنی یالهای آنان میتوانند هر تعداد رأس را احاطه کنند.
مفهوم بسطپذیر یال ابرگرافها را انعطافپذیرتر از همتایان آنها میکند. گرافهای استاندارد، تنها میتوانند روابط بین موجودیتهای زوج مثل دو دوست در شبکهی اجتماعی را نشان دهند که در آن هر شخص با یک رأس نشان داده میشود؛ اما برای نمایش رابطهی بین بیش از دو نفر مثل عضویت مشترک در یک گروه، هر یال باید بیش از دو نفر را دربر بگیرد که ابرگرافها این امکان را فراهم میکنند.
بااینحال، تطبیقپذیری ابرگرافها با هزینه همراه است و بهسختی میتوان ویژگیهای سراسری ابرگرافهای متفاوت با گرافهای معمولی را اثبات کرد. برای مثال، مسئلههای رنگآمیزی یال در ابرگرافها دشوارتر میشوند. هدف این سناریوها رنگآمیزی کل یالهای موجود در یک گراف یا ابرگراف است؛ بهطوریکه هیچ دو یالی که در یک رأس یکدیگر را ملاقات میکنند، رنگ یکسان نداشته باشند. حداقل تعداد رنگهای موردنیاز برای رنگآمیزی بهعنوان شاخص رنگی گراف شناخته میشود.
احتمال اردوش و فابر و لواز مسئلهای رنگآمیزی دربارهی نوع مشخصی از ابرگراف است که یالهای آن همپوشانی کمینه دارند. در چنین ساختارهایی که به ابرگرافهای خطی معروفاند، هیچ دو یالی اجازهی همپوشانی در بیش از یک رأس را ندارند. براساس پیشبینی، شاخص رنگی ابرگرافی خطی هرگز بیش از تعداد رأسها نخواهد بود. بهبیانبهتر، اگر ابرگراف خطی نُه رأس داشته باشد، یالهای آن صرفنظر از اینکه چگونه ترسیم شوند، با بیش از نُه رنگ نمیتوانند رنگآمیزی شوند. تعمیم بینهایت احتمال اردوش و فابر و لواز اثبات آن را دشوار میسازد. هرچ تعداد رأسهای ابرگراف افزایش پیدا کنند، روشهای ترکیب یالهای حلقوی آنها هم افزایش خواهند یافت.
سه ابرگراف بینهایت
اگر روی صفحهای بهصورت ناخودآگاه خطوطی را ترسیم کنید و به ابرگرافی خطی برسید، شاخص رنگی ابرگراف کمتر از تعداد رئوس خواهد بود؛ اما سه نوع ابرگراف بینهایت وجود دارند که این حد را نقض میکنند. در نوع اول، هر یال تنها دو رأس را به یکدیگر وصل میکند. به این نوع گراف گراف کامل گفته میشود؛ چراکه هر زوج رأس با یک یال به یکدیگر وصل میشوند. گرافهای کامل با تعداد رئوس فرد، شاخص رنگی ماکزیزم مجاز در احتمال اردوش و فابر و لواز دارند.
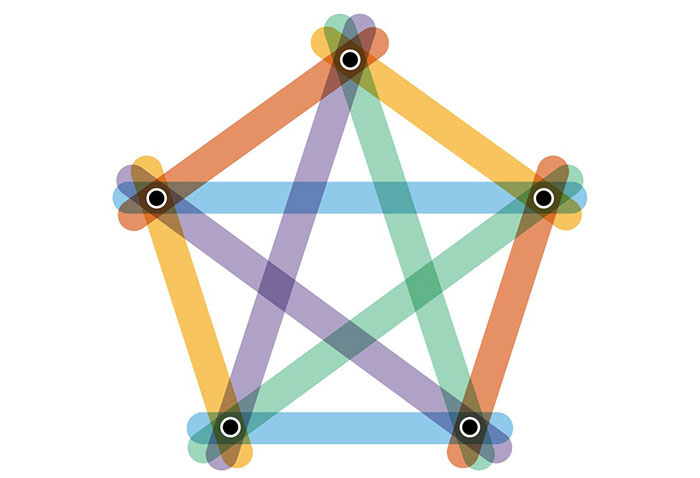
دومین نوع گراف دقیقا عکس گراف کامل است. در گراف کامل، یالها تنها تعداد کمی از رأسها را به یکدیگر وصل میکنند؛ درحالیکه در این نوع گراف تمام یالها تعداد زیادی از رأسها را به یکدیگر وصل میکنند. با افزایش تعداد کل رأسها، تعداد رئوس احاطهشدهی هر یال هم افزایش مییابد. به این نوع گراف صفحهی نگاشت متناهی گفته میشود که مانند گراف کامل شاخص رنگی حداکثر دارد.
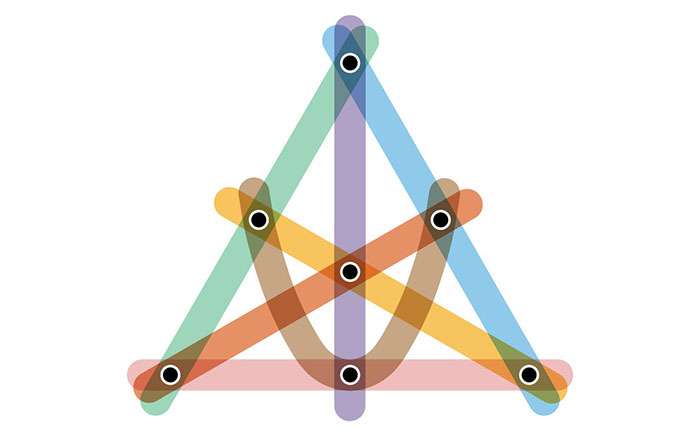
سومین نوع گراف در میانهی طیف دو گراف قبلی قرار میگیرد. در این نوع گراف، اغلب یک رأس ویژه وجود دارد که با یالهای مجزا به رئوس دیگر وصل میشود و سپس، یک یال بزرگ واحد رئوس دیگر را به یکدیگر وصل میکند.
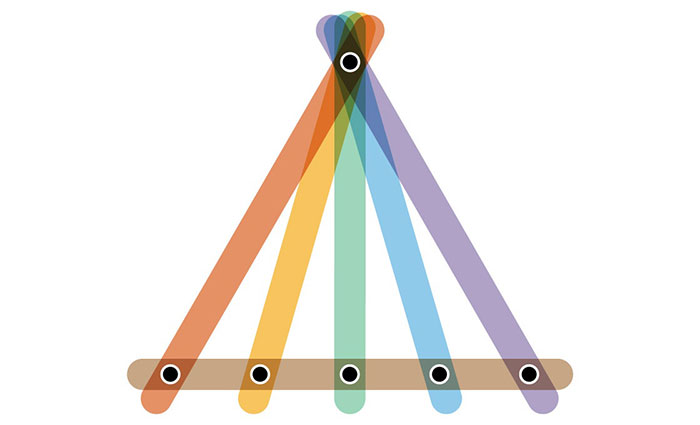
با اندکی تغییری در یکی از سه ابرگراف بینهایت، نتیجه باز هم شاخص رنگی حداکثر خواهد داشت. درنتیجه، هر کدام از سه مثال مذکور نمایندهی گروه گستردهتری از ابرگرافهای چالشی هستند که سالها است ریاضیدانان را از اثبات احتمال اردوش و فابر و لواز باز داشتهاند. وقتی ریاضیدانی با احتمالی روبهرو میشود، تلاش میکند با تعمیم الگوریتم یا روال سادهای آن را حل کند که یک رنگ را به هر یال تخصیص میدهد. چنین الگوریتمی باید برای کل ابرگرافها صدق کند و از تعداد رنگهای یکسان با رئوس برخوردار باشد.
سه گروه ابرگراف بینهایت شکلهای بسیار متفاوتی دارند؛ ازاینرو، ممکن است هر روشی که برای رنگآمیزی یکی از گروهها اثبات شود، برای دو مورد دیگر شکست بخورد. با اینکه اردوش و فابر و لواز با سه ابرگراف بینهایت آشنایی بودند، نمیدانستند گرافهای دیگر با شاخص رنگی حداکثر وجود دارند. گام بعدی دستیابی به اثباتی جدید بود که نشان میداد هر ابرگراف متفاوت با سه ابرگراف مذکور به رنگهای کمتری درمقایسهبا تعداد رأسها نیاز دارد.
مرتبسازی یالها
اثبات جدید بر روند جف کان از دانشگاه روتجر استوار بود که نسخهی تخمینی احتمال اردوش و فابر و لواز را در سال ۱۹۹۲ اثبات کرد. کان و اوستوس و گروه آنها متشکل از پژوهشگر فوقدکتری، یعنی کانگ و کلی و متکو، نتیجهی کان را بهبود بخشیدند. گرچه آنان احتمال را کاملا حل نکردند، ایدههایشان قویتر از حد انتظار ظاهر شد و متوجه شدند میتوانند احتمال را دقیقا هم اثبات کنند.
پژوهشگران کار را با مرتبسازی یالهای یک ابرگراف مشخص در چند دستهی مختلف براساس اندازهی یال آغاز کردند (تعداد رئوسی که یال میتواند به آنها وصل شود). پس از مرتبسازی، به یالهایی با رنگآمیزی سختتر روی آوردند؛ یعنی یالهایی با چند رأس. استراتژی آنان برای رنگآمیزی یالهای بزرگ مبتنیبر سادهسازی بود. آنان یالها را بهصورت رئوس گراف ساده تنظیم کردند که در آن هر یال تنها دو رأس را به یکدیگر وصل میکند. سپس یالها را با استفاده از نتایج بهدستآمده از نظریهی گراف استاندارد رنگآمیزی کردند و سپس رنگآمیزی را به ابرگراف اصلی منتقل کردند.
ریاضیدانان پس از رنگآمیزی بزرگترین یالها، به یالهای کوچکتر روی آوردند. ازآنجاکه یالهای کوچک رئوس کمتری را لمس میکنند، رنگآمیزی آنها هم سادهتر است؛ اما قراردادن آنها در اولویت آخر، رنگآمیزی را بهنوعی دشوارتر میسازد. بهمرورزمان وقتی به یالهای کوچکتر میرسیم، میبینیم بسیاری از رنگها قبلا برای یالهای دیگر بهکار رفتهاند. مؤلفان برای حل مشکل یادشده از روش ترکیبات به نام جذب استفاده کردند که اخیرا برای حل مجموعهای از مسائل به کار برده بودند.
جذب رنگها
مؤلفان از روش جذب بهعنوان راهی برای اضافهکردن تدریجی یالها در رنگآمیزی استفاده کردند. این روش تضمین میکند رنگآمیزی همیشه ویژگیهای صحیح را حفظ خواهد کرد و بهویژه برای رنگآمیزی نقاطی با همگرایی تعداد زیادی از یالهای کوچک روی یک رأس مناسب است. برای مثال، میتوان به رأس ویژهای اشاره کرد که در سومین ابرگراف بینهایت به تمام یالها وصل شده بود. خوشههای اینچنینی معمولا از کل رنگهای موجود و موردنیاز برای رنگآمیزی دقیقا استفاده میکنند.
مؤلفان برای رنگآمیزی گراف منبعی شامل یالهای کوچک ایجاد کردند و روال رنگآمیزی تصادفی را به بسیاری از یالهای کوچک باقیمانده اعمال کردند. با پیشرفت رنگآمیزی، مؤلفان از رنگهای بیاستفاده به شیوهای منتخب برای یالهای باقیمانده بهره بردند و آنها را جذب رنگآمیزیها کردند. روش جذب بازدهی روال رنگآمیزی تصادفی را بهبود میدهد. رنگآمیزی تصادفی یالها مبنایی مناسب برای تمام روالهای عمومی است؛ اما اگر برای تمام یالها اعمال شود، بیهوده خواهد بود و بعید است ترکیبی بهینه از رنگها را تولید کند. باوجوداین، اثبات اخیر انعطاف رنگآمیزی تصادفی را بهکمک روش جذب افزایش میدهد که روشی دقیقتر است.
مقالههای مرتبط:
درنهایت، مؤلفان با رنگآمیزی بزرگترین یالهای گراف با یک روش و سپس رنگآمیزی یالهای کوچکتر با روش جذب و روشهای دیگر ثابت کردند تعداد رنگهای لازم برای رنگآمیزی یالهای ابرگرافهای خطی هرگز بیشتر از تعداد رأسهای ابرگراف نیست؛ درنتیجه احتمال اردوش و فابر و لواز ثابت میشود. بهدلیل عناصر احتمالی، اثبات مؤلفان برای ابرگرافهای بزرگ با بیش از تعداد مشخصی رأس صدق میکند. این روش در ریاضیات اثبات کاملا جدیدی است؛ چراکه تعداد متناهی از ابرگرافها را حذف میکند.
مقالهی اصلی در Quanta Magazine منتشر شد.
 قوی ترین طلسمات+قویترین دعا و طلسم+قوی ترین کتاب طلسم و دعانویسی مطالب مذهبی+طلسم سیاهی و طلاق+طلسم احضار محبت معشوق+دانلود کتاب طلسم محبت و طلاق قوی
قوی ترین طلسمات+قویترین دعا و طلسم+قوی ترین کتاب طلسم و دعانویسی مطالب مذهبی+طلسم سیاهی و طلاق+طلسم احضار محبت معشوق+دانلود کتاب طلسم محبت و طلاق قوی